Economic History

Practical class #2

Ricardo Gouveia-Mendes
rgouveiamendes@ucp.pt

Invalid Date

The Malthusian Regime:
Theoretical wrap-up

The setup of the model

Assumptions

1. Output \(Y\) is produced out of land \(\overline{T}\) (fixed input) and labor \(N\) (variable input): \(Y=f(N,\overline{T})\)
2. There is no technological progress

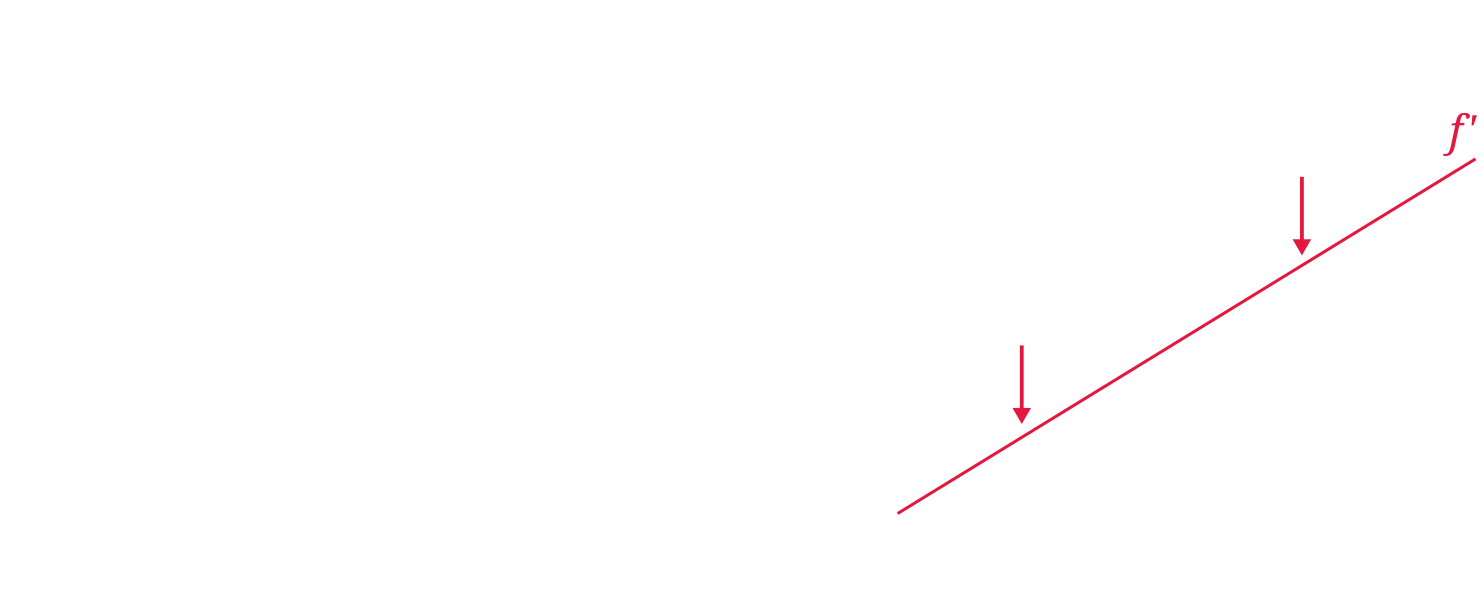
Hence, the law of diminishing returns to inputs (labor) is binding: \(f'_N>0\), but \(f''_N<0\).

For simplification, we will assume \(f'_N =0 \Rightarrow Y=\overline{Y}\).

Resulting necessary relationships

• Suppose that the population level \(N\uparrow\)
  • Output per capita \(\overline{Y}/N\uparrow\equiv y \downarrow\)
  • With everyone poorer, mortality increases and fertility decreases
  • Population enters a shrinking process
• Suppose now that the population level \(N\downarrow\)
  • The opposite will occur

• Population dynamics governs economics dynamics

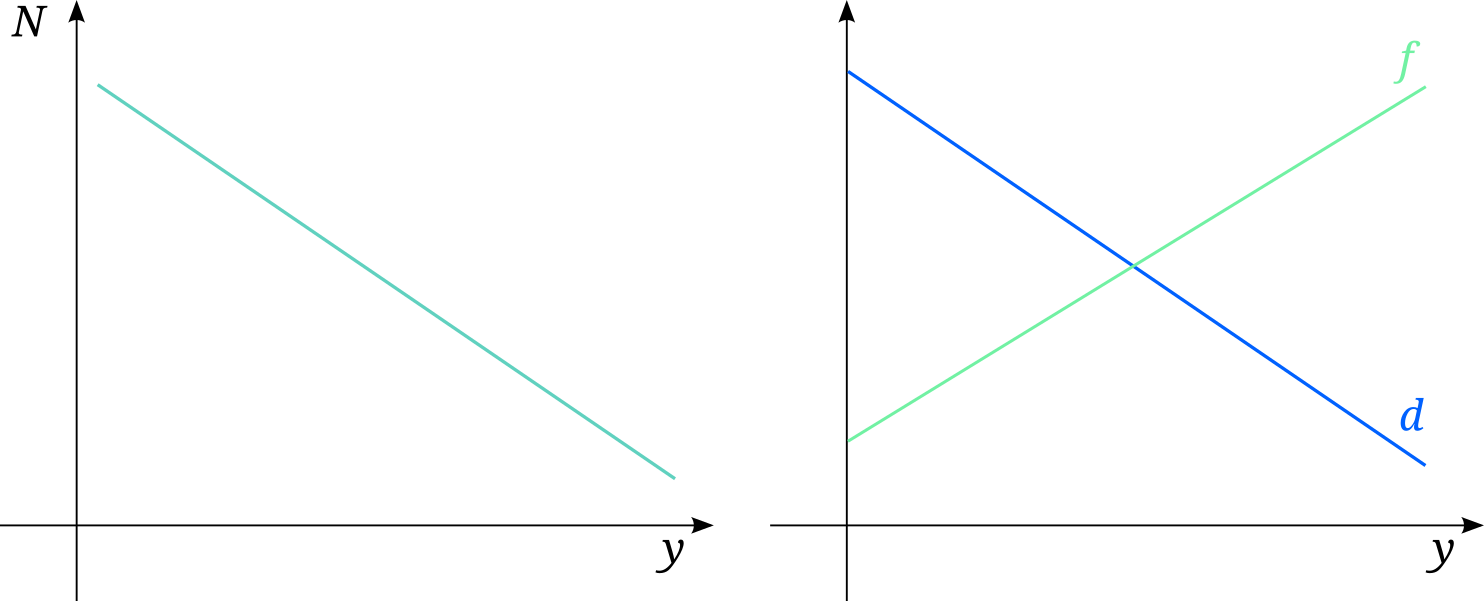
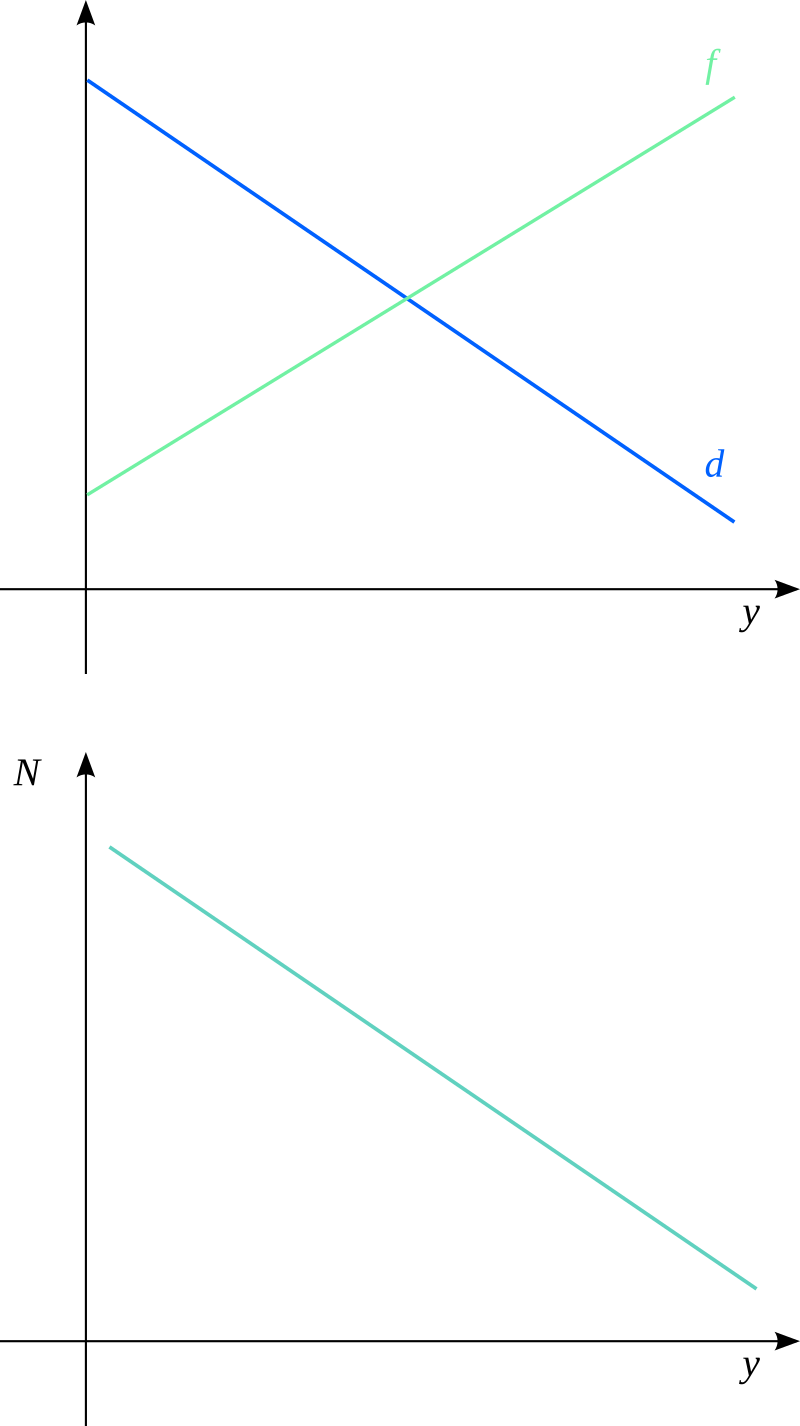
Graphically

Graphical analysis

Suppose that \(\left(y_0,N_0\right):\ d > f\)

• \(N_0\ \rightarrow\ N_1:\ N_1<N_0\)
• \(y_0\ \rightarrow\ y_1:\ y_1>y_0\)
• \(y \uparrow \Rightarrow d\downarrow,\, f\uparrow\)

Now suppose that: \(\left(y_0,N_0\right):\ d < f\)

• \(N_0\ \rightarrow\ N_1:\ N_1>N_0\)
• \(y_0\ \rightarrow\ y_1:\ y_1<y_0\)
• \(y \downarrow \Rightarrow d\uparrow,\, f\downarrow\)

Strong and Weak versions of the Model

• Previous analysis relies on: fertility and death schedules do not change with income (strong version of the model)
  • Population converges always to the equilibrium point where \(d\approx f\)
  • Apart from short-run responses to population adjustment, output per capita stagnates
  • Economies stuck in the Malthusian trap
• Against: rise in wages seen along with rises in population (e.g., England 1495-1575)

• But maybe fertility and death schedules respond to income changes (weak version of the model)
• Against: contradictory results in empirical research

The Malthusian Regime:
Exercises

Exercise 3.1 (Malthusian Island)

Imagine an island where inhabitants (initially a few) are totally isolated from the rest of the world. The only production is agriculture and this latter always follows a traditional technique of people cultivating the land without machines. The productivity of the workers (their skills) is constant over time at, say, \(A_t=A\).

Everybody always consumes the same amount of agricultural product (food).

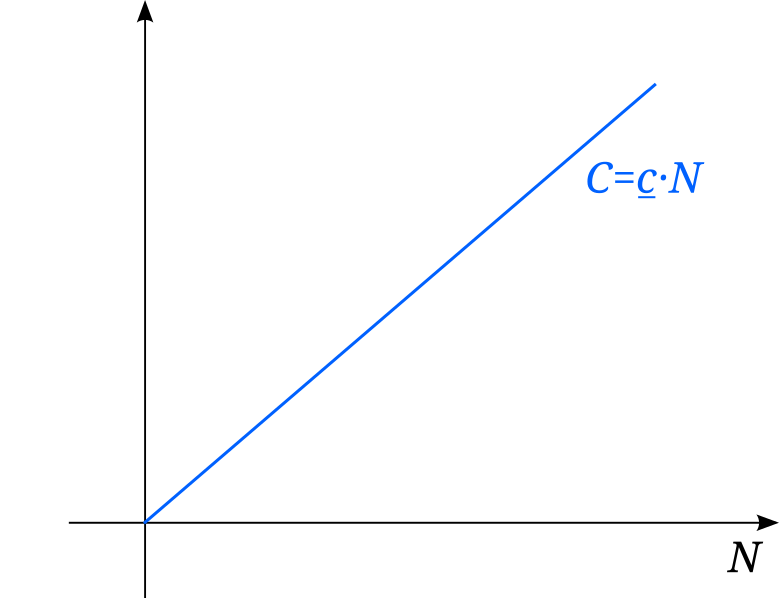
The population on the island depends on the available food. It increases at rate \(n\) when each inhabitant has more than \(\underline{c}\), the subsistence level. People die if there is less than \(\underline{c}\) per person.

Housing can be expanded indefinitely on the non-cultivable coast.

Exercise 3.1 (Malthusian Island)

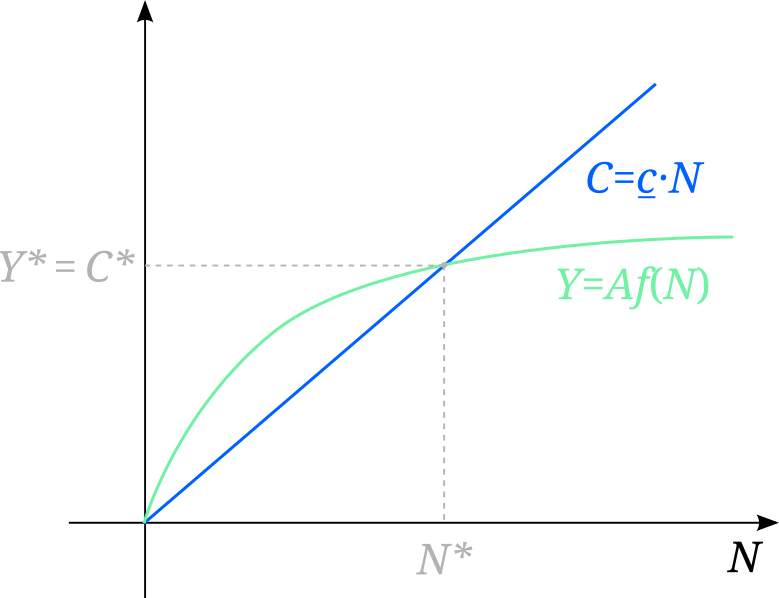
a) Consider a graph whose horizontal axis has the number of people in the island. Represent the total consumption of assuming that everybody consumes the same amount \(\underline{c}\).

b) In the same graph, represent the likely maximum possible total production of the island. Explain.

• We know that production depends only on \(N\) (so there are diminishing returns)

• Skills do not change over time, increasing productivity by a constant factor of \(A\)

• Mathematically \[Y=Af(N)\] \[f'(N)>0 \qquad f''(N)<0\]

Exercise 3.1 (Malthusian Island)

• Graphically

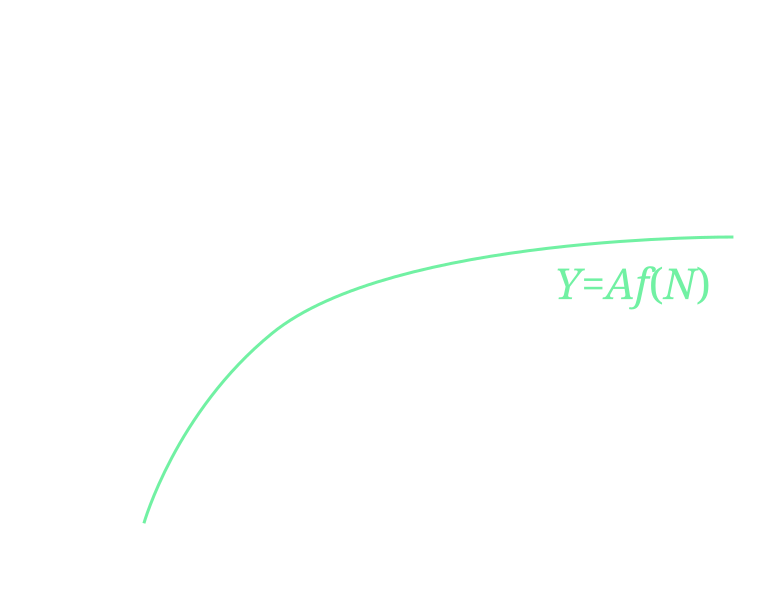
• If \(Y>C\, \Rightarrow \, N\uparrow,\, Y\uparrow\)
• If \(Y<C\, \Rightarrow \, N\downarrow,\, Y\downarrow\)
• The maximum is achieved when \[\boxed{Y^*=f(N^*)=C^*}\]

Exercise 3.1 (Malthusian Island)

c) If all the circumstances remain identical, what can you deduce for the population level of the island? Explain.

• If neither technology \(Af(N)\), nor the surviving level of consumption \(\underline{c}\) changes, population size will remain the same at \(N^*\)
• Technology is related to the shape of the production function
• Surviving level of consumption is related to the shape of the consumption function

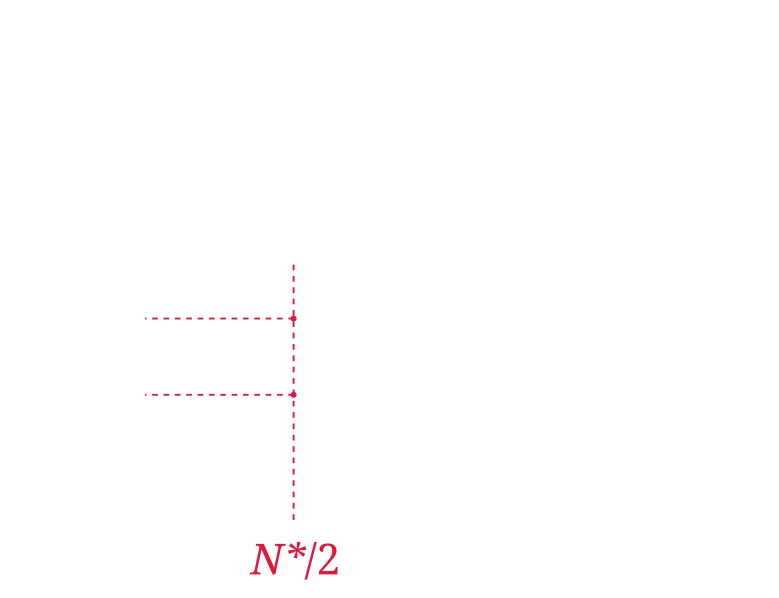
d) Suppose this economy has reached its long run equilibrium. A disease suddenly kills half of the population. What can you say about the amount of food per person available right after that episode? How does the level of ‘food per person’ evolve after?

• \(C\downarrow\) and \(Y\downarrow\)
• But \(|\Delta C|>|\Delta Y|\)
• Nutrition improves: \(N\uparrow\)
• More workforce: \(Y\uparrow\) and also \(C\uparrow\)
• These forces will stop just when \(N=N^*\) again and hence \(C=Y=Af(N^*)\)

Exercise 3.1 (Malthusian Island)

e) Suppose now that the skills of the workers can increase over time resulting in the total production growing at rate \(g\). Given the values of \(g\) and \(n\), how will ‘food per person’ evolve over time? In particular, what condition results in inhabitants having more than the subsistence level in the long run?

• So, now: \[ \begin{gathered} N_{t+1}=(1+n)N_t\\ Y_{t+1}=(1+g)Y_t \end{gathered} \]
• ‘Food per person’ in each \(t\) is given by \(y_t\equiv Y_t/N_t\)

• ‘Food per person’ evolves at a growth rate: \[\hat{y} \equiv \frac{y_{t+1}}{y_t} -1 = \frac{\frac{Y_{t+1}}{N_{t+1}}}{\frac{Y_{t}}{N_{t}}} -1\]
• Then: \[ \begin{aligned} \hat{y}&=\frac{Y_{t+1}}{Y_{t}} \times \frac{N_{t}}{N_{t+1}} -1 =\\ &= (1+g) \times \frac{1}{1+n} -1 =\\ &= \boxed{\frac{g-n}{1+n}} \end{aligned}\]

Three cases unfold:

\[\begin{aligned} y_{t+1}>y_t & &\text{if } g>n\\ y_{t+1}=y_t & &\text{if } g=n\\ y_{t+1}<y_t & &\text{if } g<n \end{aligned}\]

Exercise 3.2 (Harvest Failure)

Clark, see quote below, interprets harvest failures as a shift of the death rate. On the other hand, Bryan Caplan explains that harvest failures does not kill people but make them weaker and therefore less able to work.

In the standard graphical representation of the Malthusian framework, represent these two interpretations and derive their consequences. Explain.

In the Malthusian economy before 1800 economic policy was turned on its head: vice now was virtue then, and virtue vice. Those scourges of failed modern states – war, violence, disorder, harvest failures, collapsed public infrastructures, bad sanitation – were the friends of mankind before 1800. They reduced population pressures and increased material living standards.

— Clark (2008a)

Exercise 3.2 (Harvest Failure)

Clark

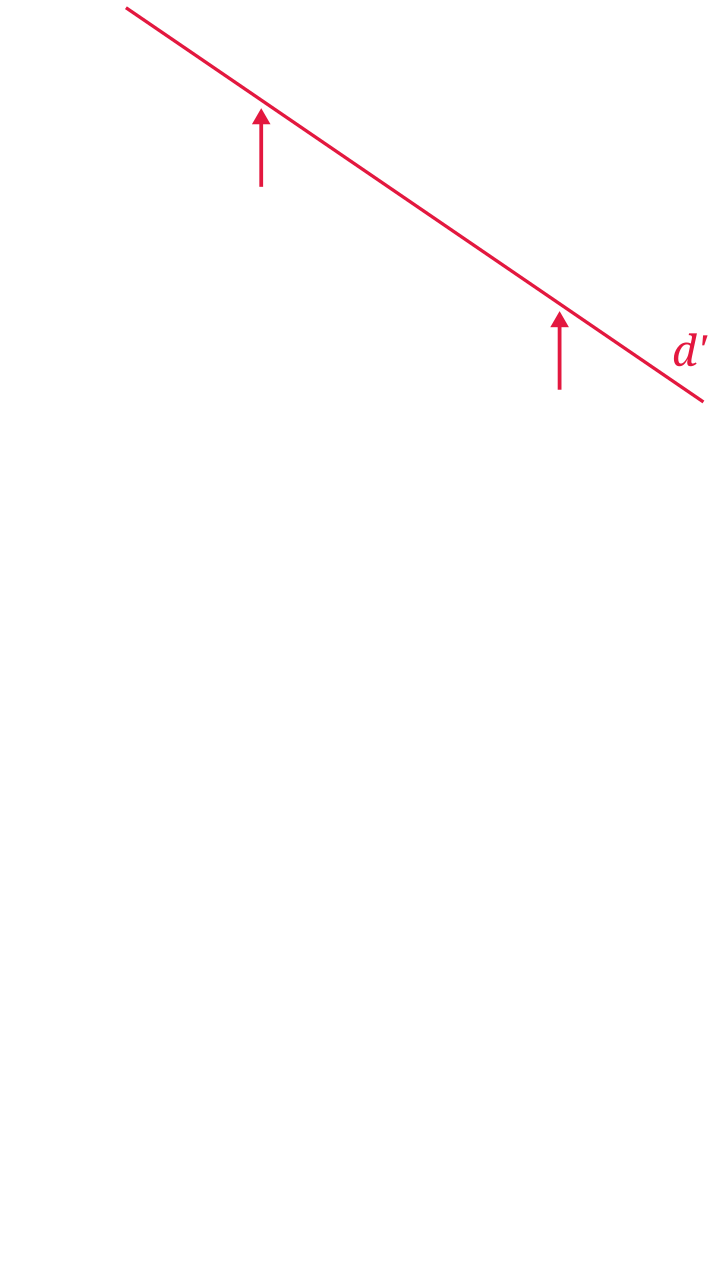
Caplan

Exercise 3.3 (Girl Power)

Consider the poem below, by Anna Bijns (1493-1575). Suppose that it is indeed informative of a new social norm of the late medieval period in some particular place, meaning that the opinion expressed therein becomes largely shared and accepted in that place.

Explain the social norm described in the poem. In a Malthusian regime, what would be the effect of this new norm? Use a graphical representation and explain.

How good to be a woman, how much better to be a man!
Maidens and wenches, remember the lesson you’re about to hear
Don’t hurtle yourself into marriage far too soon.
The saying goes: ‘where is your spouse? Where’s your honour?’
But one who earns her board and clothes
Shouldn’t scurry to suffer a man’s rod…
Though wedlock I do not decry;
Unyoked is best! Happy the woman without a man.

— Anna Bijns (1493-1575)

Exercise 3.3 (Girl Power)